Fork me on GitHub

字符串匹配的三个算法

发表于 | 分类于 |

字符串匹配的意思是给一个字符串集合，和另一个字符串集合，看这两个集合交集是多少。

  • 若是都只有一个字符串，那么就看其中一个是否包含另外一个；
  • 若是父串集合（比较长的，被当做模板）的有多个，子串（拿去匹配的）只有一个，就是问这个子串是否存在于父串之中；
  • 若是子串父串集合都有多个，那么就是问交集了。

KMP算法

KMP算法是用来处理一对一的匹配的。

朴素的匹配算法，或者说暴力匹配法，就是将两个字符串从头比到尾，若是有一个不同，那么从下一位再开始比。这样太慢了。所以KMP算法的思想是，对匹配串本身先做一个处理，得到一个next数组。这个数组是做什么用的呢？next [j] = k，代表j之前的字符串中有最大长度为k 的相同前缀后缀。记录这个有什么用呢？对于ABCDABC这个串，如果我们匹配ABCDABTBCDABC这个长串，当匹配到第7个字符T的时候就不匹配了,我们就不用直接移到B开始再比一次，而是直接移到第5位来比较，岂不美哉？所以求出了next数组，KMP就完成了一大半。next数组也可以说是开始比较的位数。

计算next数组的方法是对于长度为n的匹配串，从0到n-1位依次求出前缀后缀最大匹配长度。

比如ABCDABD这个串:

1.jpg

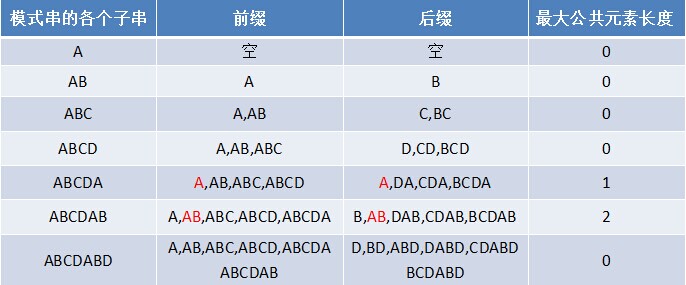
如何去求next数组呢？k是匹配下标。这里没有从最后一位开始和第一位开始分别比较前缀后缀，而是利用了next[i-1]的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

void getnext()//获取next数组

{

    int i,n,k;

    n=strlen(ptr);

    memset(next,0,sizeof(next));

    k=0;

    for(i=1;i<n;i++)

    {

        while(k>0 && ptr[k]!=ptr[i])

            k=next[k];

        if(ptr[k]==ptr[i]) k++;

        next[i+1]=k;

	//next表示的是匹配长度

    }

}

这里是按照《算法导论》的代码来写的。算法导论算法循环是从1到n而不是从0到n-1，所以在下面匹配的时候需要j=next[j+1]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

int kmp(char *a,char *b)//匹配ab两串，a为父串

{

    int i=0,j=0;

    int len1=strlen(a);

    int len2=strlen(b);

    getnext();

    while(i<len1&&j<len2)

    {

        if(j==0||a[i]==b[j])

        {   i++;j++;       }

        else j=next[j+1];//到前一个匹配点

    }

    if(j>=len2)

        return i-j;

    else return -1;

}

这里next数组的作用就显现出来了。最后返回的是i-j，也就是说，是从i位置前面的第j位开始的，也就是上面说的，next数组也可以说是开始比较的位数。也就是说，在父串的i位比的时候已经是在比子串的第j位了。

一个完整的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

#include <iostream>

#include <cstring>

#include <cstdio>

using namespace std;

const int N=100;

char str[100],ptr[100];//父串str和子串ptr

int next[100];

string ans;

void getnext()//获取next数组

{

    int i,n,k;

    n=strlen(ptr);

    memset(next,0,sizeof(next));

    k=0;

    for(i=1;i<n;i++)

    {

        while(k>0 && ptr[k]!=ptr[i])

            k=next[k];

        if(ptr[k]==ptr[i]) k++;

        next[i+1]=k;

	//next表示的是匹配长度

    }

}

int kmp(char *a,char *b)//匹配ab两串，a为父串

{

    int i=0,j=0;

    int len1=strlen(a);

    int len2=strlen(b);

    getnext();

    while(i<len1&&j<len2)

    {

        if(j==0||a[i]==b[j])

        {   i++;j++;       }

        else j=next[j+1];//到前一个匹配点

    }

    if(j>=len2)

        return i-j;

    else return -1;

}

int main(){

	while( scanf( "%s%s", str, ptr ) )

	{

        int ans = kmp(str,ptr);

        if(ans>=0)

            printf( "%d\n", kmp( str,ptr ));

        else

            printf("Not find\n");

	}

	return 0;

}

字典树算法

上面的KMP是一对一匹配的时候常用的算法。而字典树则是一对多的时候匹配常用算法。其含义是，把一系列的模板串放到一个树里面，然后每个节点存的是它自己的字符，从根节点开始往下遍历就可以得到一个个单词了。

2.jpg

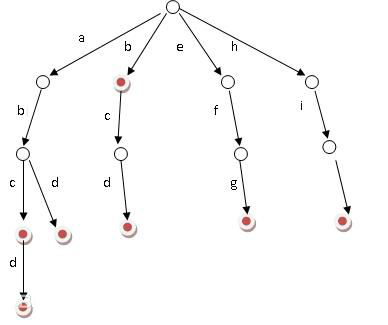
我这里写的代码稍微和上面有一点区别，我的节点tnode里面没有存它本身的字符，而是存一个孩子数组。所以当数据量很大的时候还是需要做一些变通的，不可直接套用此代码。若是想以每个节点为一个node，那么要注意根节点是空的。

树的节点tnode，这里的next[i]存的是子节点指针。sum=0表示这个点不是重点。为n>0表示有n个单词以此为终点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

struct tnode{

    int sum;//用来判断是否是终点的

    tnode* next[26];

    tnode(){

        for(int i =0;i<26;i++)

            next[i]=NULL;

        sum=0;

    }

};

插入函数：

假设字典树已经有了aer，现在插入abc,首先看a,不为空，那么直接跳到a节点里，看b，为空，那么新建，跳到b里，新建c，跳出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

tnode* newnode(){

    tnode *p = new tnode;

    for(int i =0;i<26;i++)

        p->next[i]=NULL;

    p->sum=0;

    return p;

}

//插入函数

void Insert(char *s)

{

    tnode *p = root;

    for(int i = 0 ; s[i] ; i++)

    {

        int x = s[i] - 'a';

        if(p->next[x]==NULL)

        {

            tnode *nn=newnode();

            for(int j=0;j<26;j++)

                nn->next[j] = NULL;

            nn->sum = 0;

            p->next[x]=nn;

        }

        p = p->next[x];

    }

    p->sum++;//这个单词终止啦

}

字符串比较：就是一个个字符去比呗…时间复杂度O(m)，m是匹配串长度。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

bool Compare(char *ch)

{

    tnode *p = root;

    int len = strlen(ch);

    for(int i = 0; i < len; i++)

    {

        int x = ch[i] - 'a';

        p = p->next[x];

        if(p==NULL)

            return false;

        if(i==len-1 && p->sum>0 ){

            return true;

        }

    }

    return false;

}

给个完整的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186

#include<queue>

#include<set>

#include<cstdio>

#include <iostream>

#include<algorithm>

#include<cstring>

#include<cmath>

using namespace std;

/*

    trie字典树

*/

struct tnode{

    int sum;//用来判断是否是终点的

    tnode* next[26];

    tnode(){

        for(int i =0;i<26;i++)

            next[i]=NULL;

        sum=0;

    }

};

tnode *root;

 

tnode* newnode(){

    tnode *p = new tnode;

    for(int i =0;i<26;i++)

        p->next[i]=NULL;

    p->sum=0;

    return p;

}

//插入函数

void Insert(char *s)

{

    tnode *p = root;

    for(int i = 0 ; s[i] ; i++)

    {

        int x = s[i] - 'a';

        if(p->next[x]==NULL)

        {

            tnode *nn=newnode();

            for(int j=0;j<26;j++)

                nn->next[j] = NULL;

            nn->sum = 0;

            p->next[x]=nn;

        }

        p = p->next[x];

    }

    p->sum++;//这个单词终止啦

}

//匹配函数

bool Compare(char *ch)

{

    tnode *p = root;

    int len = strlen(ch);

    for(int i = 0; i < len; i++)

    {

        int x = ch[i] - 'a';

        p = p->next[x];

        if(p==NULL)

            return false;

        if(i==len-1 && p->sum>0 ){

            return true;

        }

    }

    return false;

}

void DELETE(tnode * &top){

    if(top==NULL)

    return;

    for(int i =0;i<26;i++)

        DELETE(top->next[i]);

    delete top;

}

int main()

{

    int n,m;

    cin>>n;

    char s[20];

    root = newnode();

    for(int i =0;i<n;i++){

        scanf("%s",s);

        Insert(s);

    }

    cin>>m;

    for(int i =0;i<m;i++){

        scanf("%s",s);

        if(Compare(s))

            cout<<"YES"<<endl;

        else

            cout<<"NO"<<endl;

    }

    DELETE(root);

    return 0;

}

AC自动机

字典树是一对多的匹配，那么AC自动机就是多对多的匹配了。意思是：给一个字典，再给一个m长的文本，问这个文本里出现了字典里的哪些字。

这个问题可以用n个单词的n次KMP算法来做(效率为O(n*m*单词平均长度))，也可以用1个字典树去匹配文本串的每个字母位置来做(效率为O(m*每次字典树遍历的平均深度))。上面两种解法效率都不高，如果用AC自动机来解决的话，效率将为线性O(m)时间复杂度。

AC自动机也运用了一点KMP算法的思想。简述为字典树+KMP也未为不可。

首先讲一下acnode的结构：

与字典树相比，就多了个fail指针对吧，这个就相当于KMP算法里的next数组。只不过它存的是失配后跳转的位置，而不是跳转之后再向前跳了多少罢了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

struct acnode{

    int sum;

    acnode* next[26];

    acnode* fail;

    acnode(){

        for(int i =0;i<26;i++)

            next[i]=NULL;

        fail= NULL;

        sum=0;

    }

};

插入什么的我就不说了，记得把fail置为空即可。

这里说一下fail指针的获取。fail指针是通过BFS来求的。

看这么一张图

3.jpg

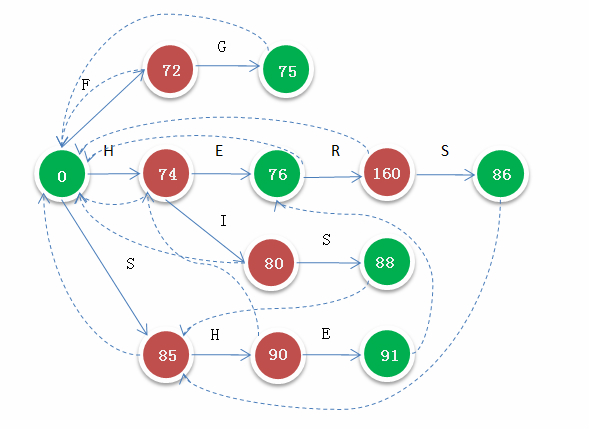
图中数字我们不用管它，绿色代表是终点，虚线就是fail指针了。我们可以看到91 E节点的fail指针是指向76 E 的，也就是说执行到这里如果无法继续匹配就会跳到76 E那个节点继续往后匹配。我们可以看到它们前面都是H，也就是说fail指针指向的是父节点相同的同值节点（根节点视为与任何节点相同）。我们要算的是在一个长文本里面有多少个出现的单词，这个fail指针就是为了快速匹配而诞生的。若文本里出现了HISHERS,我们首先匹配了HIS,有通过fail指针跳到85 S从而匹配SHE，再匹配HERS。fail指针跳到哪里就代表这一点之前的内容已经被匹配了。这样就避免了再从头重复判断的过程。

在函数里，当前节点的fail指针也会去更新此节点的孩子的fail指针，因为父节点相同啊，而且因为它是此节点的fail指针，这两个节点的父节点也相同啊~所以一路相同过来，就保证fail指向的位置前缀是相同的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

void getfail(){

    queue<acnode*> q;

	for(int i = 0 ; i < 26 ; i ++ )

	{

		if(root->next[i]!=NULL){

			root->next[i]->fail = root;

			q.push(root->next[i]);

		}

	}

    while(!q.empty()){

        acnode* tem = q.front();

        q.pop();

        for(int i = 0;i<26;i++){

            if(tem->next[i]!=NULL)

            {

                acnode *p;

                p = tem->fail;

                while(p!=NULL){

                    if(p->next[i]!=NULL){

                        tem->next[i]->fail = p->next[i];

                        break;

                    }

                    p=p->fail;

                }

                if(p==NULL)

                   tem->next[i]->fail = root;

                q.push(tem->next[i]);

            }

        }

    }

}

给个完整的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280

#include<queue>

#include<set>

#include<cstdio>

#include <iostream>

#include<algorithm>

#include<cstring>

#include<cmath>

using namespace std;

/*

    ac自动机

*/

struct acnode{

    int sum;

    acnode* next[26];

    acnode* fail;

    acnode(){

        for(int i =0;i<26;i++)

            next[i]=NULL;

        fail= NULL;

        sum=0;

    }

};

acnode *root;

int cnt;

acnode* newnode(){

    acnode *p = new acnode;

    for(int i =0;i<26;i++)

        p->next[i]=NULL;

    p->fail = NULL;

    p->sum=0;

    return p;

}

//插入函数

void Insert(char *s)

{

    acnode *p = root;

    for(int i = 0; s[i]; i++)

    {

        int x = s[i] - 'a';

        if(p->next[x]==NULL)

        {

            acnode *nn=newnode();

            for(int j=0;j<26;j++)

                nn->next[j] = NULL;

            nn->sum = 0;

            nn->fail = NULL;

            p->next[x]=nn;

        }

        p = p->next[x];

    }

    p->sum++;

}

//获取fail指针，在插入结束之后使用

void getfail(){

    queue<acnode*> q;

	for(int i = 0 ; i < 26 ; i ++ )

	{

		if(root->next[i]!=NULL){

			root->next[i]->fail = root;

			q.push(root->next[i]);

		}

	}

    while(!q.empty()){

        acnode* tem = q.front();

        q.pop();

        for(int i = 0;i<26;i++){

            if(tem->next[i]!=NULL)

            {

                acnode *p;

                if(tem == root){

                    tem->next[i]->fail = root;

                }

                else

                {

                    p = tem->fail;

                    while(p!=NULL){

                        if(p->next[i]!=NULL){

                            tem->next[i]->fail = p->next[i];

                            break;

                        }

                        p=p->fail;

                    }

                    if(p==NULL)

                        tem->next[i]->fail = root;

                }

                q.push(tem->next[i]);

            }

        }

    }

}

//匹配函数

void ac_automation(char *ch)

{

    acnode *p = root;

    int len = strlen(ch);

    for(int i = 0; i < len; i++)

    {

        int x = ch[i] - 'a';

        while(p->next[x]==NULL && p != root)//没匹配到，那么就找fail指针。

            p = p->fail;

        p = p->next[x];

        if(!p)

            p = root;

        acnode *temp = p;

        while(temp != root)

        {

           if(temp->sum >= 0)

            /*

            在这里已经匹配成功了，执行想执行的操作即可，怎么改看题目需求+

            */

           {

               cnt += temp->sum;

               temp->sum = -1;

           }

           else break;

           temp = temp->fail;

        }

    }

}

int main()

{

    cnt = 0;

    int n;

    cin>>n;

    char c[101];

    root = newnode();

    for(int i = 0 ;i < n;i++){

        scanf("%s",c);

        Insert(c);

    }

    getfail();

    int m ;

    cin>> m;

    for(int i = 0;i<m;i++){

        scanf("%s",c);

        ac_automation(c);

    }

    cout<<cnt<<endl;

    return 0;

}
扫描二维码，拯救贫困山区大学生！
-------------本文结束感谢您的阅读-------------